DANICA STATION

二分查找

5/2/2022 算法

参考资料：

二分查找有几种写法？它们的区别是什么？ (opens new window)

# 何为二分查找

  1. 将搜索区间以中位值为界，划分成两个区间。
  2. 然后将中位值与目标值做比较，如果中位值比目标值大，即目标值处于左区间，缩小右边界至中位值；若中位值比目标值小，即目标处于右区间，缩小左边界至中位值。
  3. 以新的左右边界为搜索区间，重新计算中位值，重复以上步骤，直至左右区间重叠。即左区间等于右区间

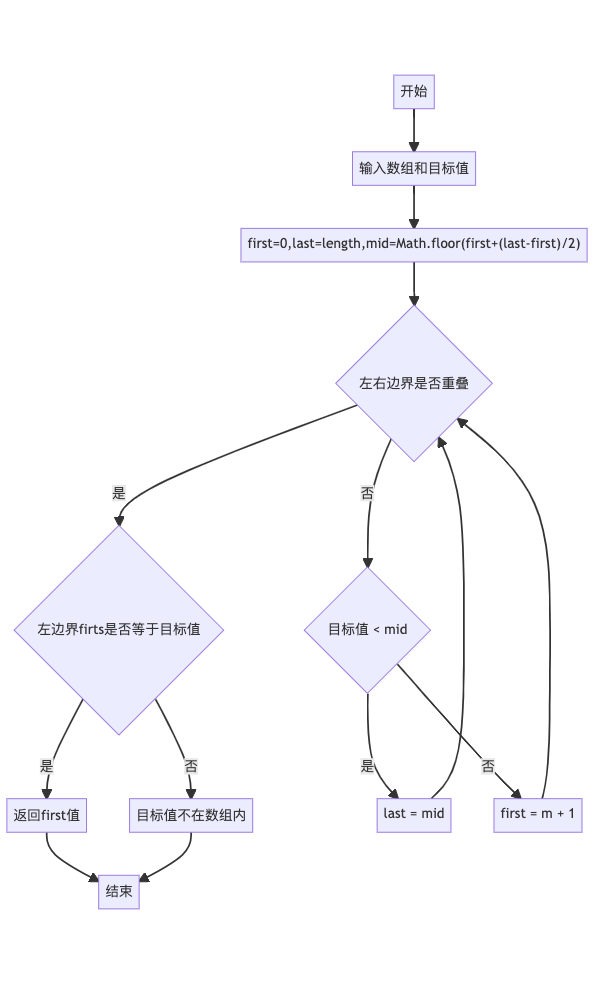
# 流程图

flowchart TB
S[开始]-->I[输入数组和目标值]
I --> C["first=0,last=length,mid=Math.floor(first+(last-first)/2)"] 
C --> D{左右边界是否重叠}
D-->|是|E{左边界firts是否等于目标值} 
E-->|是|返回first值 --> 结束
E-->|否|目标值不在数组内 --> 结束
D-->|否|D2{"目标值 < mid"}
D2-->|是|F["last = mid"]-->D
D2-->|否|G["first = m + 1"]-->D
1
2
3
4
5
6
7
8
9
10

output

# 各步骤注意点

  1. 明确左右界限和中间值 first为0，last为length（因为区间为左闭右开，即实际搜索范围为lenght-1） 中间值为first + （last-first）/2
  2. 在左右区间不重叠的循环条件内将目标值与中位值作比较 左右区间不重叠，说明搜索范围仍未覆盖全数组。
  3. 根据比较结果缩小边界范围
  • 目标值等于中间值：查找结束，返回中间值下标
  • 目标值小于中间值：mid 变为新的right边界（右开，mid值未检查，即不在搜索区间）
  • 目标值大于中间值：mid+1 变为新的left边界（因为左闭，mid值已经检查过）

# 相关题目

704 (opens new window) 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

  • 解题思路：一道非常标准的二分搜索，目标值存在时，返回first，目标值不存在时，返回-1（因为区间设置左闭右开，最后一步的比较落在左边界，所以返回first）
  • 时间复杂度： O(log n)，其中 n 是数组的长度。

278 (opens new window) 你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。 假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。 你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

  • leetcode评论区解题思路： 具体地，将左右边界分别初始化为 1 和 n，其中 n 是给定的版本数量。设定左右边界之后，每次我们都依据左右边界找到其中间的版本，检查其是否为正确版本。如果该版本为正确版本，那么第一个错误的版本必然位于该版本的右侧，我们缩紧左边界；否则第一个错误的版本必然位于该版本及该版本的左侧，我们缩紧右边界。 这样我们每判断一次都可以缩紧一次边界，而每次缩紧时两边界距离将变为原来的一半，因此我们至多只需要缩紧O(logn) 次。

  • 解题思路：这道题没有直接给出一个可以作比较的target值，而是需要调用isBadVersion(version)函数，通过返回值来判断是否要继续循环。

  • 时间复杂度： O(log n)，其中 n 是其中 n 是给定版本的数量。

  • 空间复杂度：O(1)。我们只需要常数的空间保存若干变量

35 (opens new window) 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。

  • 解题思路：704的变型，需要考虑目标值不存在于数组中时的情况
  • 时间复杂度：O(log n)， n 为数组的长度。二分查找所需的时间复杂度为 O(logn)。
  • 空间复杂度：O(1)。我们只需要常数的空间保存若干变量
Last Updated: 5/3/2022, 3:33:50 AM